Diseño a profundidad (circuito)

En este capítulo trataremos con todo detalle y minucia el diseño del circuito al que está conectada la tarjeta ESP-32. Se espera un conocimiento con buenos fundamentos de electrónica para tener un buen seguimiento de esta parte. No se tocarán temas de programación sino únicamente de electrónica.

El simulador con el que se realizó buena parte del diseño fue Proteus sin embargo, la alternativa en línea de Falstad Circuit será la mejor opción para presentarlo en este texto.

Acondicionamiento de señal

Como ya se trabajó en la parte de diseño, en esta sección estamos intentando darle un acondicionamiento a una señal eléctrica la cual desconocemos su origen. Hay unas pocas cosas que tenemos que tener en consideración al momento de diseñar este dispositivo:

1. Tendremos dos terminales de medición, como cualquier oscsiloscopio.
2. El acondicionamiento de señal tiene que transformar los voltajes de las terminales de entrada en voltajes que se encuentren en un rango de operación seguro para la ESP-32. (0V a 3.3V con respecto a la tierra de la tarjeta)
3. Es indispensable poder caracterizar el voltaje sin la necesidad de predicciones en software, es decir, la información entregada por el circuito de acondicionamiento es la única información de la que podremos generar más información.
4. La información sumistrada por medio del circuito de acondicionamiento tiene que ser suficiente para calcular los valores del voltaje entre las terminales de medición haciendo uso de un algoritmo replicable en cualquier intervalo de voltaje entre esas terminales. Con esto quiero decir, no podemos hacer uso de una X fórmula para calcular ese voltaje cuando el voltaje es negativo y de una fórmula Y cuando el voltaje sea positivo (por ejemplo).

Hay una serie de puntos adicionales que ya son más bien buenas prácticas que requisitos:

5. De usar componentes no lineales (condensadores, inductores, transistores etc.) es indispensable que se mantenga la seguridad de la tarjeta ESP-32 por encima de los componentes de acondicionamiento.
6. De usar componentes no lineales el circuito tiene que operar en un rango seguro en cuanto a su frecuencia. Es decir, no podemos permitir la formación de armónicos en el circuito en el rango de frecuencias que esperamos poder medir.
7. El dispositivo idealmente se tiene que poder alimentar con un solo cable o una sola fuente de energía. En nuestro caso, ya que estamos trabajando con un cable USB como alimentación de la tarjeta ESP-32, la recomendación es mantenerse en el rango de 0[V] a 5[V] con respecto a la tierra de la tarjeta. Esto quiere decir hay que tener MUCHÍSIMO cuidado al momento de trabajar con voltajes negativos.
8. El dispositivo no puede poner en riezgo la integridad de la tarjeta ESP-32 al momento de encendido o apagado inesperado. Esto quiere decir, todos los estados transitorios tienen que estar contemplados y corregidos. Esto es especialmente importante al momento de considerar diseño con baterías.

Implementación con solo resistores

Podemos partir de la implementación que habíamos propuesto previamente. Habíamos propuesto un sistema partiendo de un divisor de voltaje (los resistores R1 y R2) al cual introducimos una desviación de voltaje por medio de un tercer resistor (resistor N). Determinamos que necesitaremos de dos arreglos de estos tres resistores, un sistema A (R1_A, R2_A, RN_A) y un sistema B (R2_A, R2_B, RN_B).

Para realizar el modelado matemático de estos sistemas de resistores podemos trabajar con los esquemas siguientes; partiendo del diseño original crearemos una descomposición de los voltajes en el nodo RN a partir de el análisis por fuentes independientes. Podemos también realizar simplificaciones por resistores paralelos.

Circuito interactivo

Para calcular el valor de los resistores hicimos uso del método de fuentes de voltaje linealmente independientes. Como por diseño sabemos que el resistor de tierra va a tierra, no es necesario realizar el análisis con este resistor.

A partir de estos esquemitas podemos continuar con el análisis para cada una de las fuentes independientes (el voltaje introducido en R1 y el voltaje introducido en N). El voltaje introducido en R1 será uno que llamaremos "V_ref" ya que es el voltaje de referencia de 3.3 V en la tarjeta ESP-32. El voltaje introducido en N lo llamaremos "V_T" ya que es el voltaje de la terminal de lectura del osciloscopio. "V_1" y "V_2" serán los voltajes que contribuye cada una de estas fuentes independientes.

Para la fuente linealmente independiente en R1 (V_Ref) tenemos:

Para la fuente linealmente independiente en N (V_T) tenemos:

Esquemas realizados en OneNote

Así, que podemos caracterizar el voltaje presente en el nodo RN (tanto para la terminal positiva como para la negativa, en el diseño llamados terminal A y B):

\[ V_{RN} = V_{1} + V_{2} \]

\[ V_{RN} = V_{Ref} \frac{N || R_{1}}{N||R_{2} + R_{1}} + V_{T} \frac{R_{1}||R_{2}}{R_{1}||R_{2} + N} \]

Donde el operador || significa "resistor equivalente paralelo".

Podemos simplificar estas expresiones para convertirlo en una expresión únicamente dependiente de sumas y multiplicaciones:

\[ V_{RN} = V_{Ref} \frac{N R_{2}}{N R_{2} + N R_{1} + R_{1} R_{2}} + V_{T} \frac{R_{1} R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Hay que recordar que para nuestro sistema, N, R1 y R2 estarán todos determinados, el valor de V_ref es conocido (3.3V) y el valor de V_RN es el valor que leeremos con el ESP-32 por lo que el único valor que tendremos que determinar será el valor de V_T. Para conseguir esto únicamente hay que despejar:

\[ (V_{RN} - V_{Ref} \frac{N R_{2}}{N R_{2} + N R_{1} + R_{1} R_{2}}) \frac{R_{1} R_{2} + N R_{1} + N R_{2}}{R_{1} R_{2}} = V_{T}(V_{RN}) \]

Parece un poco aparatoso pero la realidad es que como todos los valores son constantes, por esto, todo se podrá simplificar a un par de números reales. De hecho, a simple vista se puede ver que ya existen ciertos factores que se pueden simplificar sin demasiados trucos algebráicos.

Ya que tenemos un modelo para describir el voltaje de la terminal T a partir del voltaje del nodo RN, que recordar, ya tenemos una serie de lineamientos que tenemos que cumplir para que nuestro osciloscopio se comporte como queremos; habíamos establecido qué comportamiento queríamos en los puntos límite del voltaje que consideramos operativo "V_Max" y "V_Min" de los cuales también deducíamos un voltaje "V_cero".

Recordando rápidamente:

\[ V_{RN}(V_{Min}) = 0[V] = V_{Min} * K_{Atenuación} + C_{Ajuste} \] \[ V_{RN}(V_{Max}) = 3.3[V] = V_{Max} * K_{Atenuación} + C_{Ajuste} \] \[ V_{RN}(V_{cero}) = 1.65[V] = V_{cero} * K_{Atenuación} + C_{Ajuste} \] \[ V_{Terminal} \in (V_{min}, V_{max})\]

Aquí tenemos una serie de requerimientos por cumplir y, por diseño, tenemos que determinar varias de ellas para poder determinar el sistema. En realidad, no es difícil ver que la parte de

\[ V_{Min/Max} * K_{Atenuación} + C_{Ajuste} \]

la vamos a tener que sustituir por la definición que ahorita obtuvimos para el voltaje en RN en función del voltaje de la terminal T en el resistor N.

Por facilidad de diseño se decidió que el voltaje mínimo fuera el mismo voltaje pero con signo negativo que el voltaje máximo:

\[ V_{Min} = - V_{Max} \]

Esto inmediatamente (como lo descubrimos en el modelado lineal) nos determina que el valor "central" (el que llamams Voltaje "cero" en la fase de diseño) sería exactamente 1.65[V] para nuestra tarjeta ESP-32. Esto quiere decir, cuando nosotros leamos 1.65 en RN significará que el valor real de voltaje aplicado en la terminal T será de 0[V] con respecto a la tierra.

Poniendo el voltaje en el nodo RN en función del voltaje de la terminal T se describiría así:

\[ V_{RN}(V_{T}) = V_{T} * K_{Atenuación} + C_{Ajuste} \] \[ V_{RN}(0[V]) = 1.65[V] \]

En realidad estamos sobre-definiendo nuestro sistema ya que, sabiendo que nuestro sistema es lineal, únicamente necesitaremos determinar los valores del voltaje Máximo y Mínimo en la terminal T para determinar todo lo demás.

Regresando a la simplificación de nuestra caracterización de voltaje de la terminal T en función de el voltaje en RN:

\[ V_{T}(V_{RN}) = (V_{RN} - V_{Ref} \frac{N R_{2}}{N R_{2} + N R_{1} + R_{1} R_{2}}) \frac{R_{1} R_{2} + N R_{1} + N R_{2}}{R_{1} R_{2}} \]

Simplificando obtenemos:

\[ V_{T}(V_{RN}) = V_{RN} \frac{R_{1} R_{2} + N R_{1} + N R_{2}}{R_{1} R_{2}} - V_{Ref} \frac{N}{R_{1}} \]

Si deciéramos obtener el voltaje en RN en función del voltaje de la terminal en vez de el voltaje de la terminal en funcion de el voltaje en RN nos quedaría algo muy parecido al sistema que propusimos de:

\[ V_{RN}(V_{T}) = V_{T} * K_{Atenuación} + C_{Ajuste} \]

Comprobémoslo para convencernos que el sistema es correcto:

\[ V_{RN}(V_{T}) = V_{T} \frac{R_{1} R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} + V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Resulta bastante convincente que en efecto estamos caracterizando el fenómeno correcto.

Ya que llegamos a este punto es necesario decidir si nuestras restricciones de diseño serán los voltajes mínimos y máximos o si serán los resistores que podemos utilizar para crear nuestra K de atenuación y nuestro C de ajuste.

Como decisión de diseño, personalmente recomiendo considerar los voltajes máximos y mínimos que uno se va a encontrar como la variable de mayor peso. Los resistores se puede comprar por un precio relativamente accesible y así cambiar el diseño por completo, sin embargo, los voltajes que encontraremos en el mundo están más o menos determinados y es bastante fácil construir a partir de esa información.

Por ejemplo, el voltaje de la electricidad en un enchufe común es de 127[V] RMS en México. Esto quiere decir que estaríamos trabajando con un voltaje Pico a Pico de 359.2 [V], en realidad el voltaje que se suministra en el país es bastante más inestable de lo que nos gustaría por lo que valdría la pena agregar un buen margen de seguridad; pensemos que el máximo voltaje que nos podríamos encontrar fuera uno Pico a Pico de 500 [V] solo para tener suficiente margen de error y garantizar la seguridad de nuestro dispositivo.

En este sentido, podríamos crear un sistema de resistores para atenuación de grandes voltajes (como el voltaje suministrado por un enchufe). Al mismo tiempo tendríamos que crear un sistema que nos diera atenuación para voltajes de uso de laboratorio (voltajes entre -20[V] y +20[V], por ejemplo).

Así tendríamos dos pequeños arreglos de resistores con los cuales podríamos medir prácticamente cualquier voltaje a nuestro alcance sin tener que sufrir una atenuación excesiva en voltajes pequeños.

Entonces, determinemos los resistores necesarios:

Personalmente me gusta comenzar con la ecuación que describe el voltaje "cero" ya que por medio de ese podemos poner rápidamente un resistor en función de los otros dos. Esto es gracias a que podemos obviar la influencia del voltaje de la terminal T.

\[ V_{RN}(V_{T}) = V_{T} \frac{R_{1} R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} + V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Sustituyendo el voltaje en la terminal T por cero (ya que asumimos que en este punto no estamos dando ningún voltaje) esperamos obtener un voltaje en RN de 1.65[V]:

\[ V_{RN}(0) = 1.65 = V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Cambiando por el valor del voltaje de referencia de operación (3.3) obtenemos una manera rápida de poner un resistor en función de los otros.

\[ V_{RN}(0) = V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Pensando en sustituir el resistor R1:

\[ R_{1} = \frac{N R_{2} * \frac{V_{Ref}}{V_{RN}} - N R_{2}}{R_{2} + N} = \frac{N R_{2}(\frac{V_{Ref}}{V_{RN}} - 1)}{R_{2} + N} \]

Tenemos que recordar que en este escenario V_Ref es 3.3[V] y V_RN es 1.65[V] por lo que podemos sustituir de una vez y volver a simplificar:

\[ R_{1} = \frac{N R_{2}(\frac{3.3}{1.65} - 1)}{R_{2} + N} = \frac{N R_{2}(2 - 1)}{R_{2} + N} = \frac{N R_{2}}{R_{2} + N}\]

¡Nada mal!

Hagamos brevemente un análisis del resultado aquí obtenido. Si nos fijamos, el valor de R1 lo acabamos de determinar como el circuito paralelo entre R2 y N. Revisemos rápidamente si esto tiene sentido.

Dado que estamos anticipando que cuando el voltaje sumistrado en T sea de 0[V] esperaríamos que el voltaje en el nodo RN sea exactamente el voltaje que se le está suministrando al Resistor 1 por medio del nodo del VRef. Es decir, el resistor equivalente entre R2 y N debería de ser igual a la resistencia en R1. Parece ser que en efecto, tiene sentido al menos en este escenario.

Ahora podemos sustituir el Resistor 1 en alguna otra de nuestras ecuaciones y deberíamos obtener alguna otra caracterización; pensemos en describir R2 a partir de N en la ecuación usada para el voltaje máximo:

\[ V_{RN}(V_{Max}) = V_{Max} \frac{R_{1} R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} + V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Sustituimos el valor del Resistor 1 por su equivalente descrito en términos de R2 y N:

\[ R_{1} = \frac{N R_{2}}{R_{2} + N}\]

\[ V_{RN}(V_{Max}) = V_{Max} \frac{\frac{N R_{2}}{R_{2} + N} R_{2}}{\frac{N R_{2}}{R_{2} + N} R_{2} + N \frac{N R_{2}}{R_{2} + N} + N R_{2}} + V_{Ref} \frac{N R_{2}}{\frac{N R_{2}}{R_{2} + N} R_{2} + N \frac{N R_{2}}{R_{2} + N} + N R_{2}} \]

Ahora intentaremos poner R2 en términos de N, V_Rn(V_max), V_ref y V_Max. Haciendo algo de álgebra obtenemos que:

\[ N = \frac{R_{2}(2 V_{RN} - V_{Max} - V_{Ref})}{V_{Ref} - 2 V_{RN}}\]

Es difícil identificar de manera inmediata algo que nos revele que la información que obtuvimos aquí sea la correcta, sin embargo, podemos convencernos ligeramente con el análisis dimensional del resultado obtenido. Tenemos que:

\[ Resistencia = Resistencia * \frac{Voltaje}{Voltaje} \]

Esto nos puede dar al menos cierto nivel de garantía que nuestro análisis no está tan mal.

Podemos hacer unos pocos cambios para intentar dejar los números resultantes de las restas como positivos ya que quizá eso nos ayude a interpretar los valores obtenidos:

\[ N = R_{2} \frac{-(2 V_{RN} - V_{Max} - V_{Ref})}{-(V_{Ref} - 2 V_{RN})} = R_{2} (\frac{V_{Max} + V_{Ref} - 2 V_{RN}}{ 2 V_{RN} - V_{Ref}}) \]

Tampoco es demasiado visible pero parecería que podemos asumir que el valor del factor entre paréntesis será un número positivo siempre que nos encontremos dentro de nuestro intervalo de voltaje. Si este número resultara negativo estaríamos metidos en un tremendo problema ya que no existen resistores con valor negativo.

Analisemos por partes, nominador y denominador:

En el nominador, por diseño V_Max es siempre más grande que V_RN, V_Ref también lo es durante todo nuestro intervalo de voltajes de operación así que, por esta parte vamos bien, esto es sin importar el valor de V_RN (el cual, hay que recordar que depende de V_T). El único valor en el que V_RN y V_Ref pueden ser iguales es cuando estemos aplicando en V_T un voltaje igual a V_Max.

Es importante recordar, V_RN es siempre función del voltaje en la terminal T (V_T) ya que V_T es el valor que hace que oscile el valor en RN, el voltaje de V_Ref es siempre constante.

\[ V_{Max} >> V_{RN} \] \[ V_{Ref} >= V_{RN} \]

Así que en el nominador todos los valores son positivos.

En el denominador tenemos que hacer uso del hecho que estamos trabajando con V_Max en la terminal T. Hay que recordar que este sistema de ecuaciones lo resolvimos simbólicamente pero en realidad:

\[ V_{RN}(V_{Max}) = V_{Ref}\]

Esto lo establecimos por diseño. De lo mismo se sigue:

\[ 2V_{RN} - V_{Ref} = 2V_{Ref} - V_{Ref} \]

Como el valor de voltaje de referencia es positivo (en nuestro caso es de 3.3[V]) igualmente tenemos un valor positivo. En realidad, con este conocimiento ya explícito podemos simplifcar toda la expresión de N en función de R2.

\[ N = R_{2} \frac{V_{Max} + V_{Ref} - 2 V_{RN}}{ 2 V_{RN} - V_{Ref}} = R_{2} \frac{V_{Max} + V_{Ref} - 2V_{Ref}}{2V_{Ref} - V_{Ref}} = R_{2} \frac{V_{Max} - V_{Ref}}{V_{Ref}}\]

¡Lindo!

Ahora ponemos rápidamente R2 en términos de N (que era la intención todo esto):

\[ R_{2} = N \frac{V_{Ref}}{V_{Max} - V_{Ref}}\]

Aquí tenemos que tomar una nueva decisión de diseño ¿Cómo determinaremos el primer resistor N de nuestro sistema?

La decisión que yo considero más prudente es determinar el resistor N a partir del voltaje máximo que se aplicará en la terminal T. Esto es porque, a pesar de que tengamos una idea más o menos buena de cuánto es el voltaje máximo que le vamos a aplicar a nuestro osciloscopio, es indispensable agregar un pámetro de seguridad adicional. En especial, con las mediciones en el mundo real, es muy muy común que el componente de tierra no sea el mismo para nuestra computadora (y por extensión en nuestra ESP-32) y la tierra del fenómeno que estamos intentando medir. Pensemos en que nuestra computadora funcionara por medio de una batería (como es el caso de las computadora portátiles), no tenemos ninguna garantía que la tierra de la batería de la pila sea la misma que la tierra de un generador se señales conectado a la corriente de un enchufe. En realidad, dado que están desacopladas ambas fuentes de voltaje, existe garantía que de que la tierra no sea la misma. Lo más probable es que el voltaje de diferencia entre tierras de la batería y la red eléctrica no sea de demasiados voltios, pero sí puede ser de unos cinco o diez voltios en condiciones no tan anómalas (apagones, generadores de emergencia, baterías de coche, etc.) Es por eso que recomiendo darle un parámetro de seguridad a nuestro diseño de al menos 20%. Tendremos una sobre-atenuación, sin embargo, nuestro modelo lo contemplará de la manera correcta.

Recordemos que es indisepensable garantizar la seguridad de la ESP-32, eso quiere decir, el voltaje presente en RN no puede ser mayor a 3.3[V] ni menor a 0[V].

Correremos riesgo de exceder los 3.3[V] cuando V_T sea máximo y de irnos por debajo de los 0[V] cuando V_T sea mínimo. Podemos plantear un circuito de ejemplo para determinar entonces nuestro primer resistor N.

Ya que R1 y R2 serán mucho más chiquitos que el resistor N, podemos considerarlos de buenas a primeras resistores de 330 ohmios ya que además van a ser resistores de valores más o menos semejantes y únicamente preocuparnos por la disipación en el resistor N. Esto nos dará un valor propuesta para el resistor N, el cual podemos multiplicar por algún factor de seguridad y, así, posteriormente cambiar el valor de R1 y R2 siguiendo la formulación que realizamos previamente donde R1 y R2 dependen de N. Ya que el voltaje de V_T es mucho mucho más grande que V_Ref podemos incluso considerar que V_Ref es una fuente apagada.

Suponiendo un resistor inicial de:

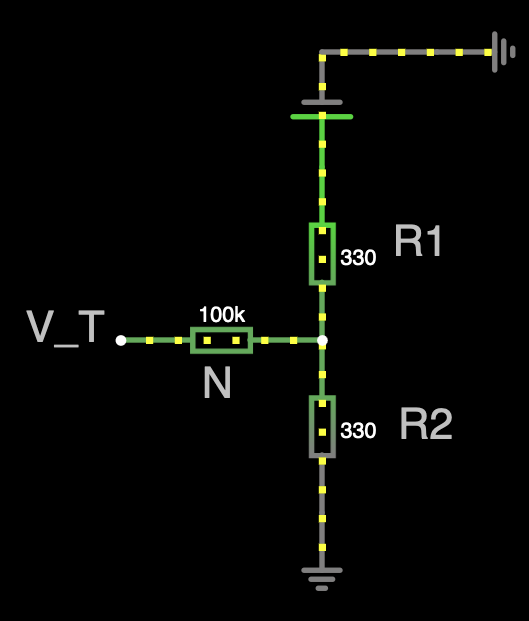
Y una simplificación haciendo análisis por fuentes independientes:

Circuito interactivo

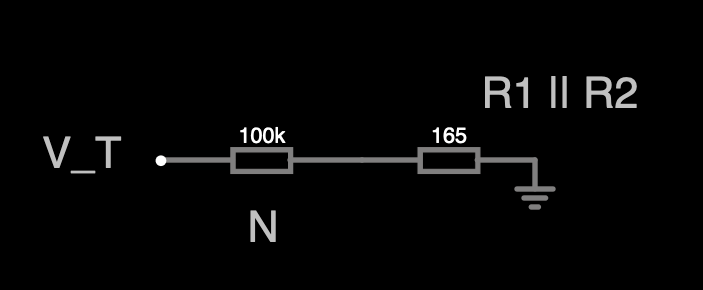
Entonces, el voltaje en RN queda caracterizado en este primer modelo propuesto: \[ V_{RN} = V_{T} \frac{R_{1} || R_{2}}{R_{N} + R1||R2} \]

Ahora necesitamos nuestro valor propuesta de V_T. Este valor a proponer, como ya dijimos, tiene que ser el valor de voltaje máximo que esperemos encontrar en nuestros escenarios de lectura. Por el bien del ejemplo y únicamente para ser congruente con los valores propuestos en la parte del armado, usaremos un valor de 50[V]. Esto quiere decir, nuesto osciloscopio será capaz de medir valores de voltaje de +50[V] y -50[V] con respecto a su tierra de manera segura y bastante exacta.

\[ 3.3 = 50 \frac{165}{R_{N} + 165} \]

De donde obtenemos el valor del resistor N:

\[ N = \frac{50 * 165}{3.3} - 165 = 2335\]

Considerando ahora en valores de resistores comerciales, podemos ver que un resitor de 3300 ohmios cumple con una tolerancia adicional de aproximadamente 30%. Así que lo definimos:

\[ N = 3300\]

Ya determinado nuestro resistor N proseguimos a determinar los resistores R1 y R2 siguiendo las fórmulas que demostramos antes:

\[ R_{2} = N \frac{V_{Ref}}{V_{Max} - V_{Ref}} = 3300 \frac{3.3}{50 - 3.3} = 233.19\]

\[ R_{1} = \frac{N R_{2}}{R_{2} + N} = \frac{3300 * 233.19}{3300 + 233.19} = 217.79\]

En efecto, obtuvimos resultados más o menos como lo esperábamos.

Ahora probemos el dispositivo que acabamos de diseñar únicamente para revisar su validés, una vez más haciendo uso de un simulador.

Circuito interactivo

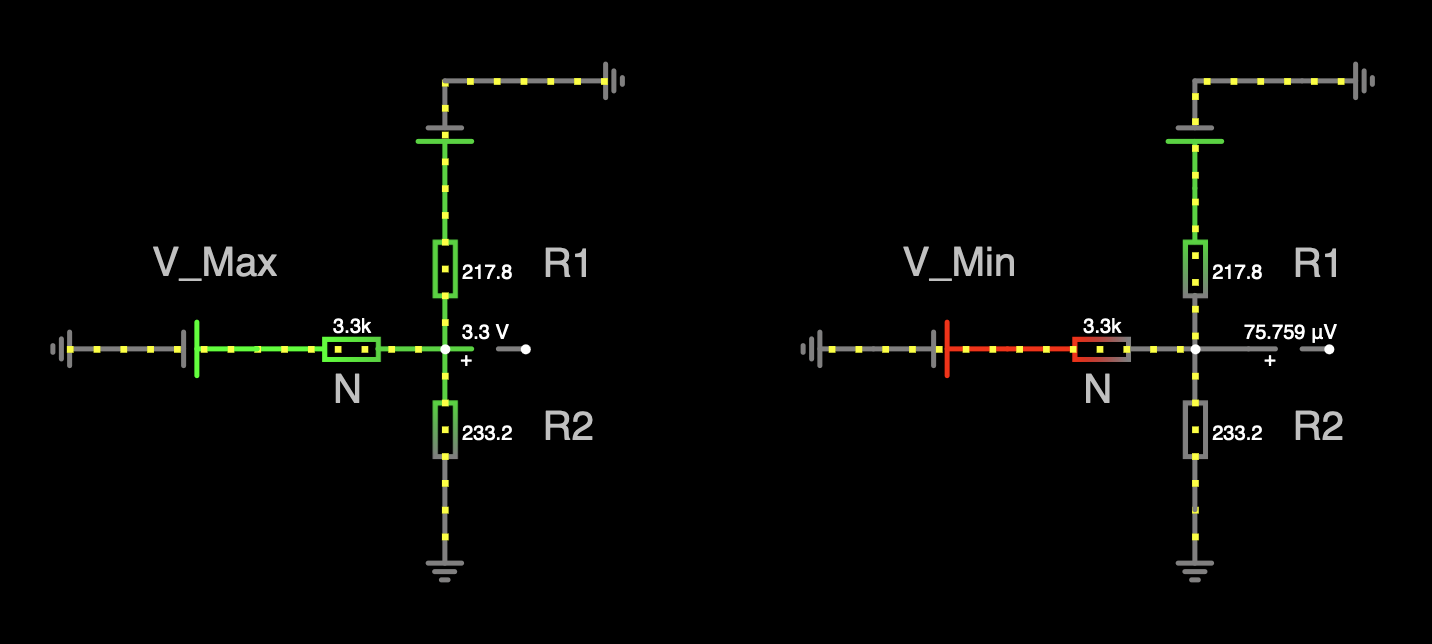
¡Lo logramos!

¡En teoría y en simulación el modelo funciona!

Es obvio que sería muy difícil conseguir resistores de 218 ohmios y de 233 ohmios. Entonces tenemos que una vez más considerar que el necesitaremos resistores comerciales.

218 lo podemos conseguir diréctamente con solo 1% de desviación si usamos uno de 220 ohmios. El de 233 lo podemos conseguir usando uno de 180 ohms y sumándole uno de 51 ohms esto nos dejaría con una desviación también menor a 1%.

Así, después de toda esta trayectoria completamos el arreglo de resistores que queríamos armar:

• N = 3300 Ohmios
• R1 = 220 Ohmios
• R2 = 180 Ohmios + 51 Ohmios

Hay que recordar que tenemos que armarlo tanto para la terminal A (positiva) como la terminal B (negativa) por lo que necesitaremos dos de cada uno.

El último paso a tomar en esta parte es deducir una fórmula fácil de calcular rápidamente para calcular el voltaje en T a partir del voltaje en RN. Si recordamos la fase anterior de diseño, cuando usamos fuentes de voltaje independientes, obtuvimos:

\[ V_{RN}(V_{T}) = V_{T} \frac{R_{1} R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} + V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}} \]

Con una fácil manipulación podemos obtener el valor del voltaje en la terminal T con respecto al voltaje de RN.

\[ V_{T}(RN) = \frac{V_{RN} - V_{Ref} \frac{N R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}}}{\frac{R_{1} R_{2}}{R_{1} R_{2} + N R_{1} + N R_{2}}}\]

Para obtener un poco más de rendimiento en la computadora podemos simplificar las divisiones:

\[ V_{T}(V_{RN}) = V_{RN}(\frac{R_{1} R_{2} + N R_{1} + N R_{2}}{R_{1} R_{2}}) - V_{Ref} (\frac{N R_{2}}{R_{1} R_{2}}) = \frac{V_{RN}(R_{1} R_{2} + N R_{1} + N R_{2}) - V_{Ref}(N R_{2})}{R_{1} R_{2}} \]

Resumido:

\[ V_{T}(V_{RN}) = \frac{V_{RN}(R_{1} R_{2} + N R_{1} + N R_{2}) - V_{Ref}(N R_{2})}{R_{1} R_{2}} \]

Cancelación del término independiente

Así, obtuvimos una caracterización del voltaje en las terminales T. Sin embargo, tenemos que recordar que no nos interesa conocer el voltaje de las terminales de manera independiente, nos interesa la diferencia de los voltajes.

Pensemos que las terminales de en las que estamos midiendo el voltaje se llamaran "A" en la terminal positiva y "B" en la negativa. (En este caso, la B se comportará más bien como el punto de referencia).

\[ V_{T_{A}} - V_{T_{B}} = (K_{V_{RN_{A}}} + C_{Ajuste A}) - (K_{V_{RNB}} + C_{Ajuste B})\]

Sin embargo, podemos analisar brevemente cuál es el valor de C de ajuste y encontrar que el valor es el mismo para ambos circuitos.

\[ V_{T}(V_{RN}) = \frac{V_{RN}(R_{1} R_{2} + N R_{1} + N R_{2})}{R_{1} R_{2}} - \frac{V_{Ref}(N R_{2})}{R_{1} R_{2}} \]

Podemos ver que únicamente el sumando del lado izquierdo es dependiente del valor aplicado en el nodo RN. El sumado del lado derecho es dependiente de los resistores y el valor de voltaje de referencia, no de la variable independiente. Como la caracterización del voltaje en el nodo RN es el mismo tanto para el nodo RNA como para el nodo RNB, podemos fácilmente simplificar.

\[ V_{T}(V_{RN_{A}}) - V_T{T}(V_{RN_{B}}) = \frac{V_{RN_{A}}(R_{1} R_{2} + N R_{1} + N R_{2})}{R_{1} R_{2}} - \frac{V_{Ref}(N R_{2})}{R_{1} R_{2}} - (\frac{V_{RN_{B}}(R_{1} R_{2} + N R_{1} + N R_{2})}{R_{1} R_{2}} - \frac{V_{Ref}(N R_{2})}{R_{1} R_{2}}) \]

Simplificado:

\[ \Delta(V_{TAB}) = V_{T}(V_{RN_{A}}) - V_{T}(V_{RN_{B}}) = \frac{V_{RN_{A}}(R_{1} R_{2} + N R_{1} + N R_{2})}{R_{1} R_{2}} - \frac{V_{RN_{B}}(R_{1} R_{2} + N R_{1} + N R_{2})}{R_{1} R_{2}}\]

\[ \Delta(V_{TAB}) = (V_{RN_{A}} - V_{RN_{B}})(\frac{R_{1} R_{2} + N R_{1} + N R_{2}}{R_{1} R_{2}})\]

Esta será la función que se utilizará para determinar el valor de la diferencia de voltajes en las fases siguientes del diseño.

Recomendaciones a futuro

Si ha llegado a este punto del manual le deseo toda la suerte y le transmito todo el entusiasmo del mundo. Como puede ver, el diseño está lleno de recovecos y errores que pueden surgir durante el proceso. Le agradezco muchísimo haberme seguido en este proceso de diseño.

No hay mayor muestra de agradecimiento que le pueda dar que dejarle consejos con respecto al diseños posteriores que quiera hacer como modificaciones a este proyecto así como proyectos personales de otra índole.

1. No lo haga.
2. De verdad, no lo haga.
3. Lo digo con toda la sinceridad del mundo, utilice diseños de otras personas en las que confíe, diseñar las cosas desde cero resulta más un proceso de crecimiento personal que algo de verdadera utilidad.

Si en verdad quiere hacerlo o lo necesita:

4. El proceso de diseño es arduo y lleno de errores, para llegar a este último diseño se tuvo que pasar por al menos otras dies propuestas de diseño, todas revisadas acompañado de gente con más experiencia que yo.
5. Siempre consulte cada paso que dé con alguien más, mientras más fácil de explicar más fácil será de diseñar también.
6. Si puede, pregúntele a profesores o gente con más experiencia que usted sobre la tecnología que conocen y la que han usado. Eso puede orientar mucho la fase de diseño además de tener cerca una persona que podrá entender los diseños propuestos sin necesidad de demasiado contexto.

Con respecto al osciloscopio

Existen muchos sitios en donde se podrían agregar soluciones más complejas según el uso que usted usuario le quiera dar:

• Convertirlo en un dispositivo autónomo (no dependiente de un cable para alimentación)
• Realisar análisis únicamente de voltajes en corriente alterna para análisis de señales
• Obviar el análisis de señales para convertir este dispositivo en un multímetro
• Agregar capacidad de medición de corriente

Hay muchas cosas que no se contemplaron en el diseño de este osciloscopio, sin embargo, queda en usted lector. Este proyecto no es bajo ninguna definición perfecto.

El diseño de electrónica analógica es difícil, intente usar los componentes que mejor conoce:

• Resistores
• Condensadores
• Amplificadores operacionales sencillos

Intente reducir el problema que quiere resolver a estos componentes antes de comenzar a usar piezas más complejas.

El único verdadero requisito en esta parte de diseño es haga "embonar" un voltaje de -Vmax a Vmax en el intervalo de 0[V] a 3.3[V]. Mi recomendación es que lo logre con una función tan sencilla como lo hicimos en esta solución:

\[ V_{RN}(V_{T}) = V_{T} * K_{Atenuación} + C_{Ajuste} \]

Si decidiera realizar un diseño en el cual ya se contemple desde el acondicionamiento de señal la resta de los voltajes entre las terminales de lectura A positiva y B negativa tendrá que tener un poco de cuidado nada más con la parte del proyecto subsecuente La programación de la tarjeta ESP-32 ya está programada contemplando la resta de voltajes entrantes por dos diferentes terminales, por lo que tendrá que realizar modificaciones ahí también.

Le deseo la mejor de las suertes; este es sin lugar a duda el lugar donde más oportunidad existe para el diseño, sin embargo, también considero que es el lugar donde más dificultades encuentra uno.